我这个例子是从90年代的一本书的Basic代码改来的,
没错就是泉光子郎编程的那个Basic(他用的是另一个版本)
一开始想用R,因为R绘散点图方便,但后来考虑到要呈现动态生成过程,便考虑了Java
多亏了普林思顿的StdDraw库,让我避免了先学几天的swing等非常手动的绘图操作
在转换成Java之后才浏览了一下别人做的,发现Python代码比书上的复杂不少。
import IntroCS_Princeton.StdDraw;
public class Lorenz {
public static void main(String[] args) {
StdDraw.setCanvasSize(1100,880);
StdDraw.setXscale(-25,27);
StdDraw.setYscale(-12,62);
StdDraw.setPenRadius(0.003);//changeable
double x=0, y=1, z=1,//changeable
interval =0.008,//also changeable
dx, dy, dz;
for (int i = 0; i <5001 ; i++) {
StdDraw.point(x,z);
// System.out.println(x+", "+z);
dx = interval*10*(y -x);
dy = interval* (x* (28 - z) -y);
dz = interval* (x*y -8*z/3);
//line
StdDraw.line(15*(x+20),3.7*z,15*(x+dx+20),3.7*(z+dz));
x += dx;
y += dy;
z += dz;
}
}
}
有趣的发现:
1 x值基本基于0对称,z值从1开始上升之后在某个正数区间上下波动;
图像生成的起点是(1,1),在中下部像一个小尾巴「参加下面」
2 递增区间(模拟dx/dy/dz)的数值对整体形状影响不大,都是蝴蝶状,但对吸引子的浓度、左右位置影响大
如图 第一个是interval 设为0.01的情况
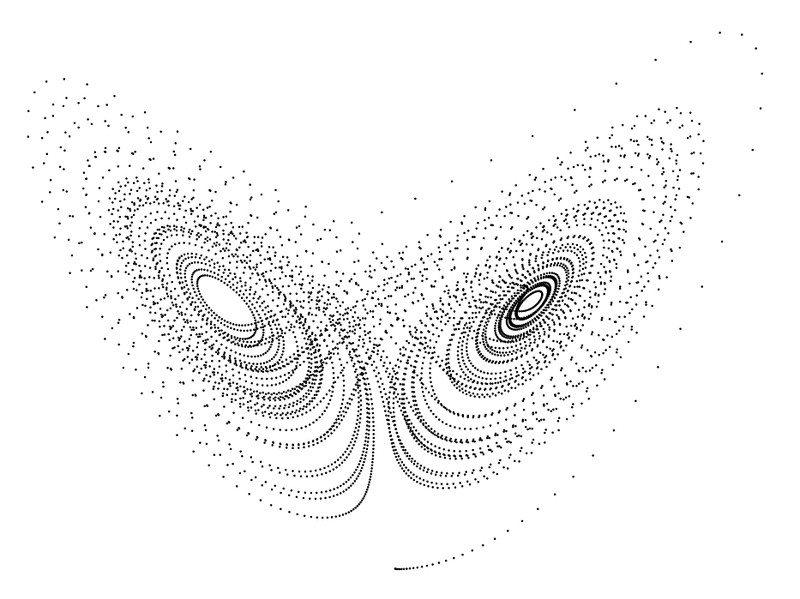
然而是改为0.001,画风不太一样了
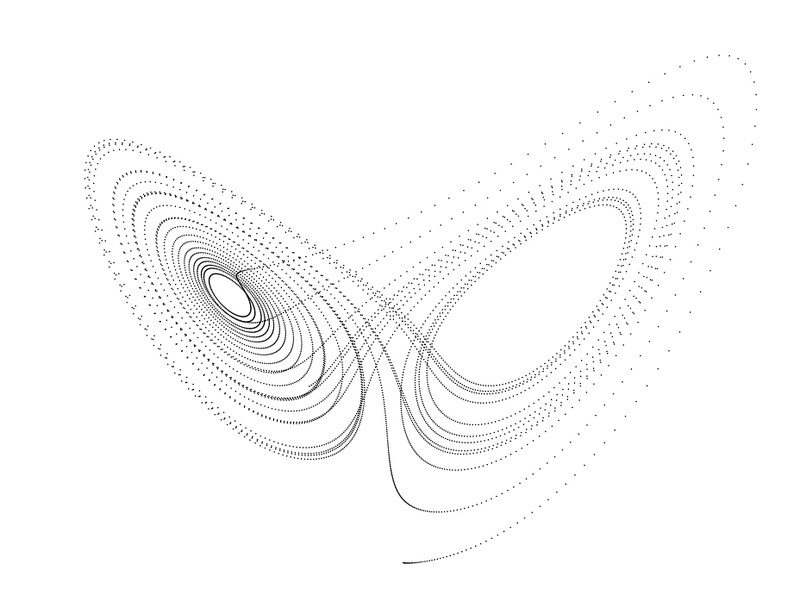
然后改成0.005
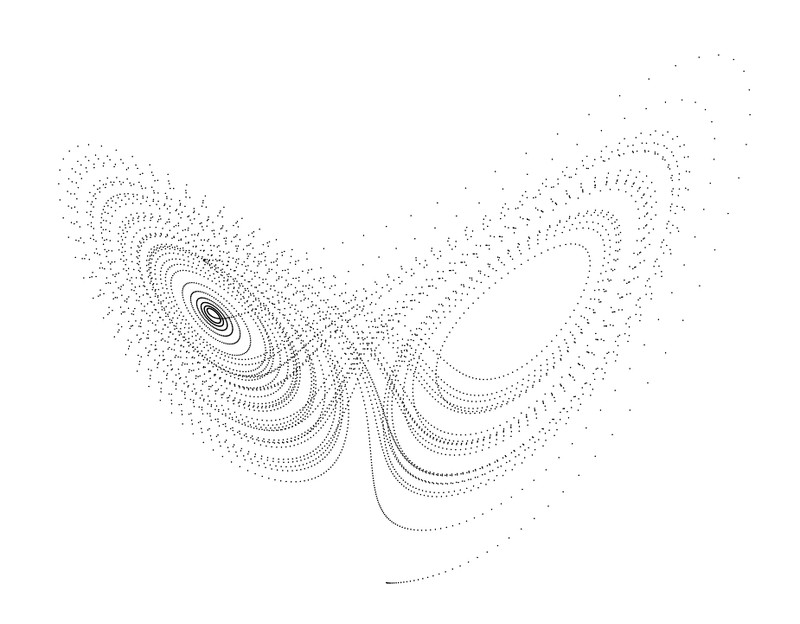
改成0.008的情况
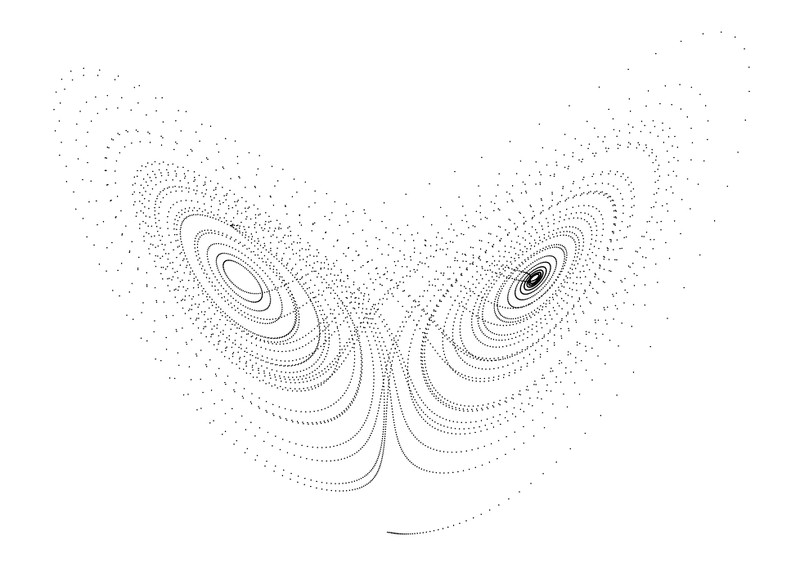
3 xyz的初始值也对图形有影响,具体情况略。
讨论:
1 混沌常常与奇妙的美结合在一起,一个非常简单的微分方程,几行代码就构造了这么一个蝴蝶状的东西。
2 这个练习是我在学神经网络时候联想起来的,这本书之前就开始看但学神经网络过程中突然对这部分内容「第5章 分形」产生了浓厚兴趣,因为二者有本质相通之处:基本构造非常简单(基于简单函数和加权比重的与或非计算 vs 3个变量的二次函数关系),但其系统变化是非常复杂而且带有“混沌”特征。
微分方程的数值解和神经网络的模式识别都可以看成传统数学/形式逻辑的“符号运算”所非常笨拙甚至无法实现的东西,比如神经网络判断银行贷款的合格条件(一个早期的金融实践),它判断出了一些金融老油条也无法发现的隐秘模式,该模式无法用基本的符号运算(比如线性回归等人类在短时间内可以完成计算的工具)实现,图像识别更是复杂,人们都几乎无法写出判别规则。
所以我下一步考虑多从这种“混沌”/“(建模与)仿真”角度感受和学习一些计算工具和计算方法,尽管有些内容归于“数学专业”与软件开发也不直接相关,这些内容所体现出的算法和数据结构的知识和要求(包括未解问题)都远远超出“计算机”专业的教程,你可以感受到栈、队列、列表这些数据结构和几个经典的访问所代表的那些内容的肤浅,真正的面向复杂系统的计算比这些复杂太多了「一个典型的应用场景可能是游戏,各种情节、图形、物理模型。。。」
参考
Lorenz洛伦兹微分方程的Python求解 陈波 https://zhuanlan.zhihu.com/p/102402046
使用Matplotlib画洛伦兹吸引子 https://blog.csdn.net/oldjwu/article/details/5037055
StdDraw: https://introcs.cs.princeton.edu/java/stdlib/StdDraw.java.html
The Nature and Power of Mathematics 1993 by Donald Davis 5.3节