Path Planning in Configuration Space
在网课 Robotics: Computational Motion Planning 里面 Lecture2.5: Trapezoidal Decomposition 提到一个分析障碍物的方法: 把障碍物用多边形拟合,比如一团什么东西近似成四边形、n边形。。。然后如有必要,每个多边形又可以再分成多个三角形。
如图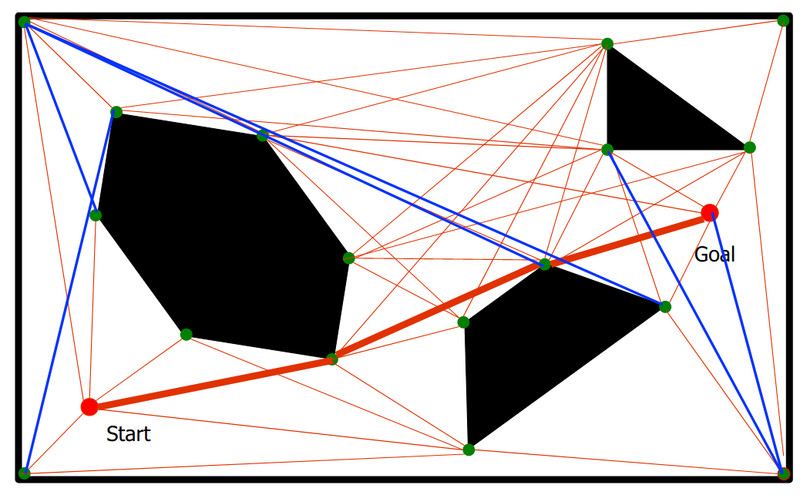
由于实际地图中的物体是非常不规则的,不存在预先设定好的三角形和多边形,于是我想到:
把不规则图形拟合成与它近似的多边形的算法是什么?「拟合成多边形的边数可以预先设定,也可以根据图像特点或计算时间/空间的条件来动态决定」
这个东西原来就是多边形识别,计算机图形学/图像处理里非常经典的问题,使用很广。
比如[1]。
由此联想起一些以前想过的算法学习方法问题: 对于没有工作经历的学生而言「对学习方向最好的引导当然是实习和工作,然而取得好的实习和工作需要一个“自启动”」全面提高算法能力的总体思路是什么?比如可以专攻某个感兴趣的领域然后以点带面提高算法和编程的能力「深度优先」,还是集中算法大类(如[2]那本有名的教程的目录)然后针对每个应用领域略做了解「广度优先」,还是?
从学习本身而言,深度优先的好处是兴趣的引领和背景知识的连续性,坏处是容易陷入死胡同,而且面临重复“造轮子”的风险——IT/工业界常常只需要系统整合;广度优先的好处是纵观全局、突出解决问题方法论而不是特定方法,坏处是容易被一些复杂的数理背景知识卡住——比如[2]里面第二章Divide-and-Conquer 用快速傅里叶变换来综合全章内容,然而理解快速傅里叶变换的算法所需要的数学和物理知识不是一般学生短期能掌握的。
从求职角度呢?我猜跟具体工作领域也有关,比如图形学和图像处理肯定要求数理基础,但互联网领域可能偏重对业务和技术框架(电商的各种业务、微软全家桶、Java EE。。。)的了解。
大家怎么看?
参考
[1] OpenCV中几何形状识别与测量 https://blog.51cto.com/gloomyfish/2104134
[2] Algorithms By Sanjoy Dasgupta and Christos Papadimitriou and Umesh Vazirani https://www.mheducation.com/highered/product/algorithms-dasgupta-papadimitriou/M9780073523408.toc.html