填一下上一篇文章剩下的坑,讲一下模p矩阵群(其实就是GL(n,Fp))的阶,当时做题的一些猜想和后来找到的证明.
前言
上次在 模n的Fibonacci的快速计算 里算出了二维的Fibonacci矩阵除了p=5的情况,阶是p^2-1;三维的"3-Fibonacci"矩阵在p=e(这是题目给的参数,不是自然常数)下的阶是e^2-1,但p是其他值是不一定是p^2-1。
赛后尝试了一下,用随机矩阵统计了一下,发现了一个神奇的规律:
| n | 阶(自乘多少次变I) |
|---|
| n=2 | p(p-1)(p+1) |
| n=3 | p(p-1)(p+1)(p^2+p+1) |
| n=4 | p(p-1)(p+1)(p^2+p+1)(p^2+1) |
| n=5 | p(p-1)(p+1)(p^2+p+1)(p^2+1)(p^4+p^3+p^2+p+1) |
| n=6 | p(p-1)(p+1)(p^2+p+1)(p^2+1)(p^4+p^3+p^2+p+1)(p^2-p+1) |
| ... | ...\ ... |
可以看出n_{i+1}项其实就是在n_i项上乘上一个多项式,这些多项式可以组成一个数列,如果把这个数列记为P的话,就是:
| P_i | 值 |
|---|
| P_0 | p ?? |
| P_1 | (p-1) |
| P_2 | (p+1) |
| P_3 | (p^2+p+1) |
| P_4 | (p^2+1) |
| P_5 | (p^4+p^3+p^2+p+1) |
| P_6 | (p^2-p+1) |
| ... | ...\ ... |
总结一下性质,以及这个数列是怎么生成的:
- P_0=p 且 P_1=p-1 ;
- 如果q是素数的话,有P_q=\sum_{i=0}^{q-1}p^i ;
- P_{a^2}=\frac{p^{a*b}-1}{P_1*P_a} ;
- P_{a*b}=\frac{p^{a*b}-1}{P_1*P_a*P_b} , a \ne b
所以如果M是一个n*n的非奇异矩阵(即行列式不为0)、p是奇素数的话,就(可能)会有:
M_{n*n}^{\prod_{i=0}^{n}P_i} = I_{n*n} \ (mod\ p)
这个是当时的猜想1,附上一段验证的代码(其实猜的大部分是对的,但还是有些代码里没考虑到的小细节错了):
# Sage
var('x')
def getOrderX(n):
P = [x, x-1]
for i in range(2, n+1):
if is_prime(i):
P.append(sum([x^j for j in range(i)]))
else:
for j in range(2, i): # brute
if i%j==0:
if j^2==i:
P.append((x^i-1)/(P[1]*P[j]))
else:
P.append((x^i-1)/(P[1]*P[j]*P[i//j]))
break
return P
def getOrder(p, n):
return int(product(getOrderX(n)).expand()(x=p))
def randMp(p, n):
while True:
mt = matrix(IntegerModRing(p), [[randrange(p) for _ in range(n)] for _ in range(n)])
if mt.det()!=0:
return mt
if __name__ == '__main__':
fail = 0
for i in range(10):
n = randint(2, 100)
while True:
p = random_prime(100000)
if p > 1: break
I = identity_matrix(IntegerModRing(p), n)
order = getOrder(p, n)
yes = True
for _ in range(10):
m = randMp(p, n)
if pow(m, order)==I:
continue
else:
print('%s\t%s\tfail' % (p, n))
print(pow(m, order))
fail += 1
yes = False
break
if yes:
print('%s\t%s\tyes' % (p, n))
print('------')
print('done!')
print('fail: %s' % fail) # 0
捣鼓一下,其实还有另一个猜想:当时统计了一下,发现其实\prod_{i=0}^{n}P_i是一个很松的界,实际测试(枚举小n和小p下的全部非奇异矩阵)的话是没有试过能到达这个阶的,而实际能达到的最大阶是:
\prod_{d|n}\phi_d(p) = p^n-1
记这个作猜想2吧(名字好像不重要:)
正文
上面说的其实是一个星期前的内容了,根据这几天搜集到的资料,发现其实有更多可以完善的地方,比如:
- 上面说的“模p非奇异矩阵的群”其实就是在\mathbb{F}_p上的一般线性群(general linear group over \mathbb{F}_p),通常记作GL(n, \mathbb{F}_p),其中n是方阵的维度,\mathbb{F}_p是指矩阵元素在域\mathbb{F}_p上(当然也可以在其他域上,不过就是另外的内容了);
- 上面说的数列P除了第0项其实是叫分圆多项式(cyclotomic polynomial),通常把它的第i项写作\phi_i(p),但那四点性质还是适用的;
网上拿“GL(n,p)”作关键字搜了一堆后,最终在这里找到“简单”的证明,还有一篇论文[1],然后有以下结论:
猜想2是对的,而且论坛的回复里一句话就证了:

根据[1]的Theorem1,
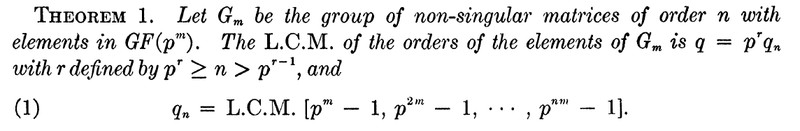
在\mathbb{F}_p上,其实就是m=1,即有:
q_n=LCM(p-1, p^2-1, ..., p^n-1)
实际上可以把分圆多项式代进去化简,即:
q_n = LCM(\prod_{d|1}\phi_d(p), \prod_{d|2}\phi_d(p), ...,\prod_{d|n}\phi_d(p) ) = \prod_{i=1}^{n}\phi_i(p)
在猜想1中,这一半是没问题的,有一个小细节问题是p^r,论文的要求是p^r \ge n > p^{r-1},而我的n是在randint(2, 100)中选的,p是在random_prime(100000)中选的,即大概率是p^1 \ge n > p^0,也即r大概率会是1
总结以上,最后的结论是:
设 \phi_i 为分圆多项式的第i项、GL(n, \mathbb{F}_p)是域 \mathbb{F}_p上的一般线性群、A \in GL_n(\mathbb{F}_p)、I是GL(n, \mathbb{F}_p)单位元,则有:
A^{p^r\prod_{i=1}^{n}\phi_i(p)} \equiv I \ \ (in\ GL_n(\mathbb{Z}_p))
其中p^r \ge n > p^{r-1};实际上,GL(n, \mathbb{F}_p)中元素的最大阶只能到:
\prod_{d|n}\phi_d(p) = p^n-1
总结
在翻资料的时候“好像”瞄到了有求GL(n, \mathbb{F}_p)特征值然后分解的,看看能不能再水一篇(逃
当初线性代数没学好啊... ...
当初抽象代数也没学好啊... ...
参考
[1] Ivan Niven, Fermat theorem for matrices, Duke Math. J. 15 (1948), 823-826
原文链接:https://tover.xyz/p/Order-GLnFp/
PS:论坛好像不支持markdown的表格?(逃