《解锁算法》导读

Bintou

《解锁算法》(Algorithms Unlocked, MIT出版社, 2013)

算法是计算机专业的核心内容，初学者往往因为学习算法的难度太大而却步，而《解锁算法》则为初学者搭建一道通往算法核心的桥梁，是一本优秀的算法导读专著。通过这本书，读者可以了解计算机解决问题的基本方法，评价算法优劣的方法，感受到算法学习的乐趣，可视为深入学习《算法导论》的先导教材。该书作者是著名教材《算法导论》的作者之一Thomas H. Cormen教授，他有丰富的算法教学经验，所以，该书内容丰富而又显得简洁易懂，适合初学者自学与阅读。推荐给计算机专业低年级的同学，甚至任何对计算机解决问题感兴趣的同学都可以阅读。

Cormen教授今年退休了，真是快，《算法导论》也要出第四版了。这个时间点，新手真的可以先看看这本《解锁算法》，在新的一年解锁新技能！

Bintou

为什么推荐《解锁算法》？

主要有以下理由：
1、首先应该吸引尽可能多的同学参与阅读马拉松，所以，难度不宜太大，篇幅不宜太长，而这本书符合这个要求。
2、体现专业的核心性，刚好算法是计算机专业核心和重点。
3、阅读马拉松以阅读为主，通过阅读带动学习，而这本书则不是传统意义的教科书，更类似科普，或者列入专业的泛读丛书。
4、我们大部分同学需要阅读全英的专业书，而这本书非常具备可读性，满足作为英语专著阅读入门书籍的要求。

应该以什么样的心态参与阅读？

1、首先，建立信心，相信自己一定能行，能啃得下，并有收获。
2、其次，也要做好有困难的准备，毕竟是英文专著，不是每一位同学都有阅读英文专著的经历。加上大家学业繁忙，各种社团活动可能也很多，都会造成障碍。
3、所以，从第二点引申出来，除了心态上，还需要做好充分的阅读计划，并切实落实自己的计划。

如何定制阅读计划

《解锁算法》的章节

根据主要内容，大致上可划分为七专题（或部分）。不包括附录、索引，全书大致是212页，内容由浅至深，建议按顺序阅读。
1、基本算法知识（第一、二章）
2、排序算法（第三、四章）
3、图算法（第五、六章）
4、字符串算法（第七章）
5、密码学算法（第八章）
6、压缩算法（第九章）
7、计算理论（第十章）

《解锁算法》的特点

根据这些特点，可把自己的计划重点放在“阅读”之上。
1、内容相对较简单。
2、论述平易近人，尽可能地压缩了严谨的数学表达。
3、篇幅较短，覆盖范围不广。
4、没有课后习题，只有建议的阅读资料。

初步计划

做一个非常保守的估算，全书阅读完，尽可能不要超过五周时间（仅代表我个人看法）。每周大概40页。或者，每周两章。考虑到第一、第二个部分相对容易，可以稍微快。具体计划可根据自己的实际进度微调，但是，依然建议阅读进度必须尽快。

若干阅读建议

如果你不是大一新生

目前参与阅读马拉松的同学有一部分同学已经有相当的基础，比如，学过《数据结构》。这时候，我建议也不要小看这本书。开始可能阅读会比较顺畅，但是，也需要注意某些被忽视的知识点，比如，书一开头就讲到的“loop invariants”（P.21）。我相信很多高年级的同学也会忽视，而作者会认为这个概念很重要。到了第五部分（密码学算法），也会遭遇一些困难。而最后的一部分《计算理论》则还是有相当多的知识点需要消化的。因此，高年级的同学，阅读的重心可以偏后，但是也要调整好心态。

如果你不是计算机专业的同学

如果你不是计算机专业的同学，那很棒，你选择参与了一件非常有意义的活动，相信你也同样会有巨大的收获。一般来说，计算机专业的同学平时的编程训练会为算法的阅读理解带来很大的促进，比如，排序、查找，这些内容很可能他们都已经碰到过。但是对非计算机专业的同学而言，也许情况并非如此，很有可能就是，这一部分同学对编程比较陌生。我的建议就是，你不一定要会编程，但是必须要动手，用笔和纸跟着作者的描述去手动计算。其次，就是要尽快熟悉读懂“伪代码”，我想，这是一个难点。第三点，心态也要调整好，这时候，这本书对外专业的同学（当然我知道某些非计算机专业的同学对计算机也非常内行，我这里是泛指）来说就不一定是简单的了，需要有攻坚心态。

0x0001

期待！华南师大图书馆的 “阅读马拉松” 也是本站非常推荐各位同学参加的活动，觉得这一次也是人文与理工科结合的一个新的突破吧。

有兴趣的同学还可以考虑加入我们的“阅马”志愿开发小组，发挥计算机所长，帮助图书馆老师们更好地去组织阅读推广活动，尝试引导更多同学静下心去读点什么～（之前有一个比较初步的构想在这里）

Chever-John

想问问深圳有没有啥校图书馆可以外借emmmmm，来实习这会儿，没有书可读，心痒啊

0x0001

Chever-John 直接搜索有 PDF 版本，看域名好像是印尼的一个大学老师分享的。

MingLLuo

作为补充笔记(未完工),有些自己组织的语言可能错误,内容还是以课本为主

What Are Algorithms and Why Should You Care?

How to Describe and Evaluate Computer Algorithms

Algorithms are a fundamental part of computer programs. Whether you are multiplying two numbers or processing images sent by spacecrafts billions of mile away, you need algorithms to solve the problem at hand correctly and efficiently.

算法在我们的生活处处可见,我们研究算法,是为了高效而又正确的解决问题,通过学习算法提高思维能力...
这里的效率有多方面的考量,占用的空间资源,运算的时间长度

Linear Search

通过顺序查找所需要的值,我们还要保证严密,在未找到数据时候返回信息,不能单认为所求必在其中

How to characterize running times

If you know a bit about actual computer architecture, you might know that the time to access a given variable or array element is not necessarily ﬁxed, for it could depend on whether the variable or array element is in the cache, in main memory, or out on disk in a virtual-memory system.

在计算机中,进行某个步骤都要一定的时间,通过求和,我们能得到关系式(包含上下界,一般对应最坏以及最好情况)
书中通过时间复杂度进行概括,不能单纯理解为使用的seconds,应该理解为运算的步骤数的数量级,为什么?不同的配置的硬件对运算的时长影响也很大,我们通过关注算法运算时间的增长量级(在较大数量级下得到结果的步骤数进行抽象)得到时间复杂度的概念

渐进符号

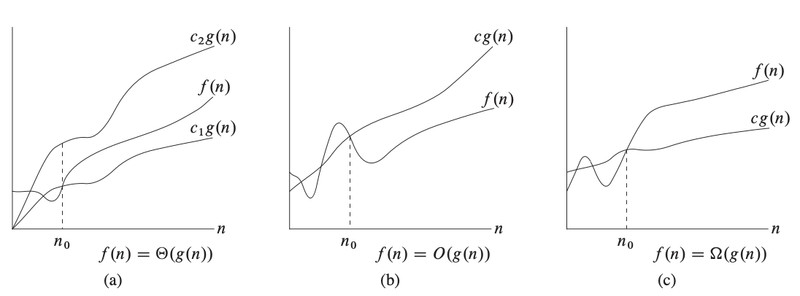
\Theta符号

\Theta{(g(n))=\{f(n)}:存在两个正数{c_1,c_2}和{n_0}使得{0\le c_1g(n)\le f(n)\le c_2g(n),n>=n_0}\}{g(n)}是f(n)的渐进紧确界(asymptotically tight bound)，

O符号

渐进上界最坏时间
O{(g(n))=\{f(n)}:在正数{c}和{n_0}得{0\le f(n)\le cg(n),n>=n_0}\}

\Omega符号

渐进下界最优时间
\Omega{(g(n))=\{f(n)}:在正数{c}和{n_0}得{0\le cg(n)\le f(n),n>=n_0}\}

o符号

无穷小量
o{(g(n))=\{f(n)}:对于任意正数{c}，存在{n_0}得{0\le f(n)< cg(n),n>=n_0}\}

\omega符号

无穷大量
\omega{(g(n))=\{f(n)}:对于任意正数{c}，存在{n_0}得{0\le cg(n)< f(n),n>=n_0}\}
PS:有时间复杂度也有空间复杂度,暂时不提及

Loop Invariants(循环不变式)

A loop invariant is a tool used for proving statements about the properties of our algorithms and programs.
Naturally, correctness is the property we’re most interested in.
We should be sure that our algorithms always produce correct results before putting them to use.

在计算机执行一个有迭代、循环的算法时,我们很难跟踪其中发生了什么(除非使用调试等技巧),很多时候会遇到未达到目标的情况下循环不终止或者提前终止的行为
因此,我们引出了Loop Invariants,它能够正确说明程序中变量的关系,在执行前为真(Initialize),执行过程也为真(Maintenance)
Termination又怎么理解

The test condition of the loop is not part of the invariant. It is what makes the loop terminate.

The loop will terminate if each time through the loop you move closer to satisfying the termination condition.

与数学归纳法很相似,但是数学归纳法多研究无穷的情况,Loop Invariants多研究数据集范围内的情况

Recursion

称作递归,需要base case才能使得其正常返回

Algorithms for Sorting and Searching

Binary Search

和高中所学的几乎没有差异,通过中位数分半缩小探查范围

Selection Sort

Insertion Sort

两者很相似,放一个插入排序的伪代码

Merge Sort

Quick Sort

将问题分而治之的排序算法
分治思想:

分划为子问题
递归的攻破问题
结合子问题的答案形成完整解

上述算法最好的平均时间复杂度为\Theta(nlgn),因为他们都是少不了元素间的比较,他们会生成一棵元素两两比较的决策树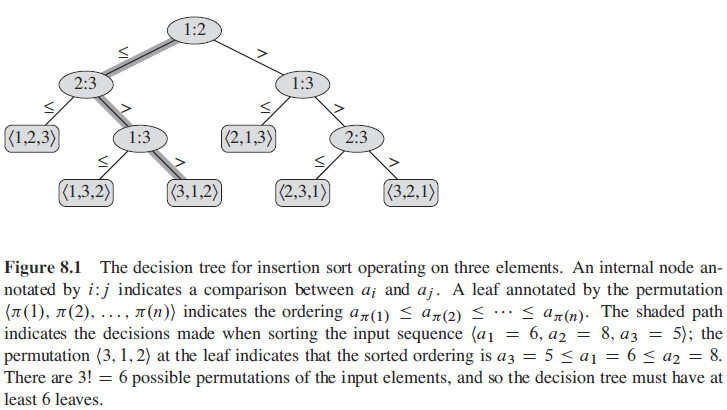

当然也存在一些线性时间的排序算法\Theta(n)
计数排序、基数排序、桶排序...

MingLLuo

MingLLuo ...

Directed Acyclic Graphs

作者借打冰球提出约束和传递，这里的单个约束我认为是两个事件具有先后顺序(A->B)，传递性是连续的约束形成的关系(A->B->C)，通过这些关系，我们能作有向图并借助算法达成我们的目的
我们可以借助邻接链表/邻接矩阵来表示有向边
在有向图中，有入度(in-degree)出度(out-degree)之分，我们图中的某个顶点i有deg(i)=id(i)+od(i)，不难发现，边的个数为总度数的二分之一(我们统计了两次边)
有人也会叫有向图为AOV(Activities on Vertices)网络
我们考虑没有环的情况

Topological sorting

拓扑排序，通过每次观察入度为0的顶点，我们能够将其移出并放入序列中，该顶点不受约束影响
上述事件不受权重影响，我们只需关注先后顺序满足要求即可，当我们遇到有权的有向图，给定无限的资源下同时执行多个任务，总时间最短为多少呢？

PERT chart(program evaluation and review technique)？

书中通过取反，将每个顶点(事件)所用的时间，转换到了两个顶点的边上，找到图中的最小值，反过来就是最大值，也是完成这道菜肴所需要的最小时间
入度为0的结点与start相连，出度为0的与finish相接。通过拓扑排序，获得序列，对每个顶点进行Relax(松弛操作)，与其相接的边通过比较更新

Shortest Paths

Dijkstra’s algorithm

它是一种边的权值非负的求单源最短路算法
核心思路是通过起点更新相邻节点的最短路径值，再寻找其中的最小值端点，这样子更新下去，每次长度次短的最短路径长度就是在尚未确定最短路径顶点中最小的(绕了点，可以看图思考🤔，书中(d)->(e)时选择了z而非x)

At the start of each iteration of the loop in step 3, shortest[v]=
sp(s, v) for each vertex v not in the set Q.That is, for each vertex v not in Q,the value of shortest[v] is the weight of a shortest path from s to v .

The Bellman-Ford algorithm

允许负权值的边但是不能存在一个负数回路
核心思路就是通过不断考虑(至多n-2次)存在的边更新源点到顶点的最小路径值，得到最优路径。我们可以在考虑一轮边缺没有更新任何最短路径的时候提前结束。
有个改进的SPFA算法,暂时没深入了解。。。

The Floyd-Warshall algorithm

针对有\无向图的算法
通过这个式子应该能让大家直观理解
令A^{(k)}[i][j]为顶点i到j，从顶点i到j最短路径的中间节点序号不大于k的最短路径长度
我们可以得到递推式
A^{(k)}[i][j]=\min\bigl\{A^{(k-1)}[i][j],A^{(k-1)}[i][k]+A^{(k-1)}[k][j] \bigr\},k=0,1,...,n-1

Bintou

为了方便大家阅读和写书评，我精选几篇网络上对该书的书评给大家参考。一篇好的书评，我认为主要在于读者能表达自己独到的观点。

Reviewed by Allen Stenger

原文链接
This is a very clearly-written, brief introduction to computer algorithms. Each algorithm is introduced with a detailed concrete example, followed by a careful statement of the algorithm. Despite its marketing, the book is not a guide for the general reader (it is too technical and jargon-laden) nor does it have much about how algorithms touch everyday life.

The big difference between this book and a text such as Cormen & Leiserson & Rivest & Stein’s Introduction to Algorithms (3rd edition, 2009, MIT Press) is that texts devote much more space to analyzing algorithm performance. This book broadens the audience by omitting most of this material, and usually just asserting the asymptotic behavior rather than deriving it. This reduces greatly the amount of mathematics needed. The intellectual rigor is no less than a textbook, but many topics are omitted. The book also has no exercises.

The book’s strength is in its step-by-step explanations of how the algorithms work. It includes a few applications, such as the GPS and secure credit card transaction applications promised on the back cover blurb, along with fax machines (compression), package delivery scheduling (shortest-path algorithms), and PERT charts (topological sort). All the treatment of applications is skimpy and seems tacked-on to a traditional abstract discussion of algorithms. In fact, the terms GPS and secure transaction are not even listed in the index. The GPS discussion only covers shortest-path algorithms, while omitting the equally-important algorithms for determining the current position. The secure transaction discussion only covers public key cryptography and not certificates or session keys.

Bottom line: A clearly-written book with many good features, but a book in search of an audience.

Allen Stenger is a math hobbyist and retired software developer. He is webmaster and newsletter editor for the MAA Southwestern Section and is an editor of the Missouri Journal of Mathematical Sciences. His mathematical interests are number theory and classical analysis. He volunteers in his spare time at MathNerds.org, a math help site that fosters inquiry learning.

Customer Review

原文链接

I am reading lot of algorithms books lately due to rekindled interest (the last time I am this motivated is during my high school days!) and the common advice is to read CLRS (C for Cormen) but the book is a 500 pound gorilla and it is neck deep in detailed Math. Imagine my delight when I stumbled on "Algorithms Unlocked" by Cormen - I call this book Baby Cormen. My background is in software engineering and I am paying my dues for 10+ years. I like math but am not in touch with it for many years; though I am currently taking steps to remedy it. So that’s the context. Here goes my review:

Pros

It has a section on "Algorithms on Strings". Out of many books that I perused (Algorithms in a nutshell, Skiena, Eva Tardos etc.), this book, CLRS, Algorithms by Sedgwick has a section on Strings. There are dedicated books on String algorithms but "string problems" appear practically in almost every software engineer's career that I think any general algorithms book should cover a basic portion of it. This one does.
Chatty but neither boring nor tedious. It uses enough words to convey the concept efficiently.
It contains math for sections on complexity but algorithm concepts are supported with pictures, sample algorithm runs. One just needs to follow logical arguments as it is explained.
All the chapters except last few pages in chapter 9, 10 are gems.
The length of the book is ₂₂₂. This cannot be overstated. The faster u reach towards the end of the book the better you will feel about yourself and the more you will like to finish it.
Pretty good paper quality and print. Love this about MIT press.
Price is cheap.
No exercises. Yes this is a good thing actually. It would have affected the flow of the book. If you need exercises then go to Big Cormen (CLRS).

Cons

Typos/Errors. 14 when I counted. I actually thought it cannot have any because some reviewer here said it was copyedited by someone who is a stickler for perfection so I didn't bother to check the errata page (my bad but only 14 errata’s is still impressive) until I stumbled on a possible typo (it turns out it is not) and tried to contact the author by going to the book's website. One should make sure to correct it in the book before reading.
Chapter 9 - section on LZW compression/decompression could have been little clearer. Chapter 10 - section on Hamiltonian cycle to Hamiltonian path reduction, subset sum reduction could have been little clearer because the explanation had more gaps in logic than usual. The author did say in the preface that he couldn't control getting into more details near the very end of the book but I felt the explanation was unclear because it is rushed than more technical details are employed.

All in all this is a solid book that treats you as an intelligent human being than a space alien or a brick.

Quora上的讨论

原文链接
在这里，一不小心就看到了《解锁算法》的作者Tom的发言，大家可以去围观。以下是其中一则评论。

Actually, Algorithms Unlocked is a good book if you, at least, care about algorithms. It neither requires hardcore math that makes you feel uncomfortable or too trivial for a real thinking. All you're expected to have is a mind for math (logical & abstract thinking), which is a really good test if you want to know whether you are potential for learning Algorithms.

On the other hand, CLRS is more suitable for a University course, which needs serious focus and research over a semester. But once again, if you passed Unlocked comfortably (and hence know some concepts), with an experienced instructor (the professor or your friends), you can shine.

In summary, read Unlocked with relax to find whether yourself a potential CS undergrad. For CLRS, a university course.

P/S: If you have any troubles understanding Algorithms, then How to think about Algorithms, by Jeff Edmons is a good place. Though it's not a reference book, it does serve to re-form (or connect the dots) your understanding about Algorithms.

Bintou

How to think about Algorithms

作者: Jeff Edmonds
出版社: Cambridge University Press
出版年: 2008-05-19
页数: 472
定价: USD 38.99
ISBN: 9780521614108

在《解锁算法》的评论中，找到一本与之类似的著作，就是Edmonds的《How to think about Algorithms》。推荐给大家。此书作者也是一位很牛的科学家。如图。可作为扩展阅读。

MingLLuo

相关资料的实时共享link：
百度网盘提取码: p1t5

Bintou

碰到阅读的疑问时，要第一时间打开勘误表看看，看是不是有人报错，这是作者给出的勘误表。

MingLLuo

在5月15日晚19:00有一场线上线下同步进行的《解锁算法》读书会，欢迎大家参与
Topic: 《解锁算法》读书分享会
时间：2022/05/15 19:00-21:00(GMT+08：00)
https://meeting.tencent.com/dw/Wq33YuEa6cO4
#会议号：362-515-425

qazxcdswe123

TL;DR 这是一本内容非常基础，整体较为简单，部分细节可能偏难，但对于非计算机科班可以不求甚解略过，比较严谨的算法科普书，推荐给所有人看，完全没问题。

正文

前

对这本书的第一印象就是，它真的在努力降低很多门槛，它降低的门槛不只是知识上“前置知识”所产生的门槛，更多的是一种心理上的畏惧所产生的门槛。前面几章看下来，真的有点像一个老奶奶给你读睡前故事哄你睡觉一样的感觉，非常的随和（也读的比较想zzz）。
这种低门槛的方式我觉得挺好的，很多时候不是能力不行，而是自己先退却了，包括阅读英文书籍也是，学了那么多年英语不用来读英语用来考试，真是浪费。
当然，it comes with a cost，那就是它前面真的啰嗦，一个查找能讲几十页，还因为太过啰嗦把我整晕了，不过对于没有程序/算法基础的人来说，也是件好事，比较符合它的定位。

中

感觉到了图论一块，就开始图穷匕见了，没有基础的我开始看着有些吃力了，不过虽说吃力，但是其实看下去也不难，看完之后有不少迷迷糊糊的直觉，但是可能真的要我严谨的写出来/证明的话，可能还是差了不少（当然可能也和它给出的大部分解释和代码都是非常口语化的表述有关系，学习的更多是思想，直觉。就这点来看的话它做的不错。）
有一点比较有趣的是，读完 Graph 两个半章才发现自己把 Vertex（顶点）和 Edge（边）搞反了。。。。。。。怪不得一直觉得看起来怪怪的，真是无语。

后

说实话，后面的 Cryptography 那章作为科普讲的是真的精彩，读的非常开心，AKS primality test and it's paper "PRIMES is in P", HOLY SHIT, nerd 的浪漫好吧，看的好 suang 哦。
但是，其他的很多地方，我觉得不行，不太喜欢，很多东西是突然提出来，come out of nowhere，讲个几页，几段，讲了点皮毛就没了，挥一挥衣袖，不带走一片云彩，看的云里雾里。
NP and P 那部分前面的科普还行，后面讲的有些迷迷糊糊，模棱两可？就没看完。

总结

虽然看的时候挺开心的，但是看完似乎又没有记住啥（摸头）
这种 bar 很低的科普书有一点不好，就是有时候不得不模棱两可的解释，后面难度高一些之后更能看出来这一点不足，没办法，定位的限制。
相对于隔壁 CLRS ，这本书真是捧你在手心里，还怕你化了（流汗黄豆
没有习题对这本书来说也是加分项吧，就是来看着玩的
总的来说还是比较推荐的。

Bintou

qazxcdswe123 阅马的金牌🏅安排上！@MingLLuo

MingLLuo

一本科普书能够受到欢迎，并且有很多人给出较高的评价，推荐给所有人看，当然没问题(滑稽🤪

对不了解算法的同学来说，这本书或许可以帮助构建部分框架，但是读这本书真的能够有成效，抑或是高效的引领他们进入算法世界？能有成效，但不能高效。这样说其实是还缺一点，读这本书的人没有明确阅读目标的话，仅仅是想稍微理解，其实可以读其他书，有且不限于《漫画算法》、《图解算法》...这些插图丰富，语气诙谐，阅读后印象可能更深
对了解算法并有深入学习的同学来说，这本书或许就是玩具，看看就好，也会用自己的视角提出更多专业性的看法
对于夹在这之间的我，我只能抱怨一句，读不懂第十章，放一放先吧(until now)

作为一本英文读物(虽然有中文，但我不说可能也没人知道，毕竟中文版叫他《算法基础：打开算法之门》，翻译成解锁算法多好😎)，假如抱着想要学习算法并且挑战接触一本英文著作的想法(这是我认为更加可取的阅读目标，PS:“挑战”一词更多的是面向没有尝试阅读英文读物的同学)翻开这本书，你会发现新大陆：

偏专业性的词语都会在上下文有所诠释
为了让你理解某个算法作者会带你进入一定的场景
似乎不用抱着词典不会就查(不会跑去看中文版(我自己就跑去看了看🥹
似乎读一本全英文的计算机科普书并不是太难，作者写过CLRS，和它相比，Algorithm Unlocked 没有用过多的数学推导，摆一堆求和符号来得出时间复杂度
...

能够具象的构建一定的理解，明白算法运行背后的逻辑，并且在读完这本书后，能够主动去阅读其他有关计算机学科的文章、书籍，是我认为阅读完这本书应该带来的“感觉”。
如果我不是学计算机的，会有“勇气”读完这本书吗，谁知道呢......